Reductions and NP-completeness
Understanding hardness through reductions
Reductions
Polynomial Time Reductions
NP-completeness can seem to be very abstract and not useful when designing algorithms. Why does it help to recognize that a certain problem can be “verified” quickly?
Well, it turns out that many of the problems mentioned above are strictly different flavors of the same problem. That is, if you can solve one of the problems quickly (in polynomial time), you would be able to solve any other problem in this list quickly as well. Karp, in his seminal paper, found 21 such problems, but today, we know of hundreds of thousands of them. These problems are known as NP-complete problems.
How was Karp able to prove that all these problems are effectively the same? This is what the idea of a reduction is. We say that some decision problem $A$ is polytime-reducible to $B$ (sometimes we use the notation $A \le_p B$) if there is some algorithm $f$ which runs in polynomial time such that
Here’s what this intuitively says. Let’s say we had a magic black box that could tell us the yes/no value of if a problem is in $B$. Then, if there is a reduction $f$ which allows us to solve $A$ by using this black box for $B$, we can say that $B$ is strictly “harder” than $A$. Because, if we are ever able to solve $B$ with some algorithmic black-box, our reduction would immediately give us an algorithm for solving $A$.
So here’s what Karp was able to prove. He took $\texttt{CLIQUE}$, and then showed how it could be solved via $\texttt{IS}$. Then he took $\texttt{IS}$, and showed how it could be solved via $\texttt{HP}$. Then he took $\texttt{HP}$, and showed how it could be solved via $\texttt{TSP}$. Finally, he took $\texttt{TSP}$, and showed how it could be solved with $\texttt{CLIQUE}$. In other words, Karp took his 21 problems and made a reduction chain something along the lines of
thereby showing
which says that if we could solve any one of these problems, we could solve them all.
Note, this works because reductions are transitive, $\texttt{A} \le_p \texttt{B}$ and $\texttt{B} \le_p \texttt{C} \Rightarrow \texttt{A} \le_p \texttt{C}$, which is true because the reduction from $\texttt{A}$ to $\texttt{B}$ can be composed with the reduction from $\texttt{B}$ to $\texttt{C}$ to get a reduction from $\texttt{A}$ to $\texttt{C}$.
NP-completeness
Seeing this, a natural question is “is there a hardest problem in P?”, or “is there a hardest problem in NP?”. With reductions, we can answer this. First, what does it mean to be the “hardest” problem?
We say that a problem $A$ is “harder” than any problem in NP if
for all $B \in \text{NP}$. Usually, we call the set of all such hard problems NP-hard, and so we would say that the $A$ above satisfies $A \in \text{NP-hard}$.
However, not all of these “hard” problems are interesting. For example, one such problem $A$ could be the problem “always output the correct answer of a nondeterministic Turing machine” and it can clearly trivially solve all the problems in NP. However, this problem is definitely not in NP.
So, to make this more interesting, we define a class of problems that are the hardest within NP. That is, they are both NP-hard, and they are in NP. These problems are called NP-complete.
Cook-Levin Theorem
Theorem: $\texttt{3SAT}$ is NP complete Proof: First we need to show $\texttt{3SAT} \in \text{NP}$. This is pretty simple—given some boolean formula, our witness can be an answer to the boolean formula, and our verifier can be an algorithm that plugs in that answer and checks if it evaluates to true or not.
The second thing we need to show is that, $\texttt{3SAT} \in \text{NP-hard}$. This, unfortunately, is pretty difficult. How do we show that every single problem in NP can be reduced to a polynomial sized instance of $\texttt{3SAT}$? Thankfully, Cook and Levin were able to do it, with some interesting trick involving simulating Turing machines and their tapes. Their construction is pretty complicated though, so we will spare you the details here.
Fortunately, thanks to Cook and Levin’s hard work, showing a problem is NP-hard is no longer as time-consuming and difficult! Now, since we know $\texttt{3SAT}$ is NP complete, if we want to show $\texttt{A}$ is NP-complete it suffices to first show $\texttt{A} \in \text{NP}$, and then to find some reduction
This is because $\texttt{3SAT}$ is harder than every problem, and $\texttt{A}$ is harder than $\texttt{3SAT}$, so $\texttt{A}$ is harder than every problem!
Below is the picture to keep in your head.
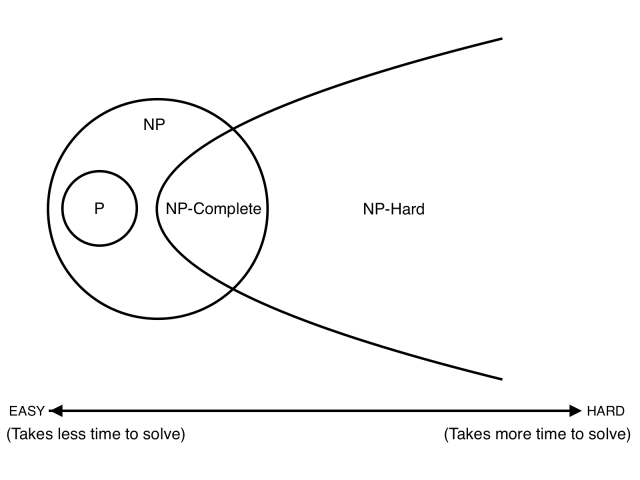
It’s important to note that the picture above is what computer scientists generally agree is probably true. It’s still possible that we will be able to find some fast algorithm to solve an NP-complete or NP-hard problem, in which case, the three sets collapse to give $\text{P = NP = NP-complete}$.
Let’s go take a slight detour to analyze a specific reduction between $\texttt{3SAT}$ and $\texttt{CLIQUE}$, and see what it allows us to say.
Reduction of 3SAT to Clique
Reduction: We want to convert instances of 3CNF formulas to instances of graphs in polynomial time. In the constructed graph, cliques of a specified size correspond to satisfying assignments of the 3CNF formula. So a solution for a $k$-clique problem can be directly used as a solution for the 3CNF problem.
- Let $\phi = (a_1 \vee b_1 \vee c_1) \wedge (a_2 \vee b_2 \vee c_2) \wedge … \wedge (a_k \vee b_k \vee c_k)$
- Reduce this 3CNF into an undirected graph $G$ by grouping the vertices of $G$ into $k$ groups of 3 vertices, each called a triple
- Each triple corresponds to one of the clauses in $\phi$. Each vertex in a triple corresponds to a literal in the corresponding clause.
- Connect all vertices by an edge except (1) vertices in the same triple or (2) vertices representing complementary literals, e.g., $x$ and $\neg x$.
function Reduce3SATtoKClique(phi):
V ← empty set
E ← empty set
for i from 1 to k:
t_i ← {a_i, b_i, c_i}
V ← V ∪ t_i
for each u in V:
for each v in V:
if u ≠ v AND not in same triple AND not complementary:
E ← E ∪ {u, v}
return G = (V, E)
Example: Here’s an example on the boolean formula
Notice that almost all the edges are included except those within a triplet, and those going between the negation of the same literal (like $x_1$ and $\neg x_1$).
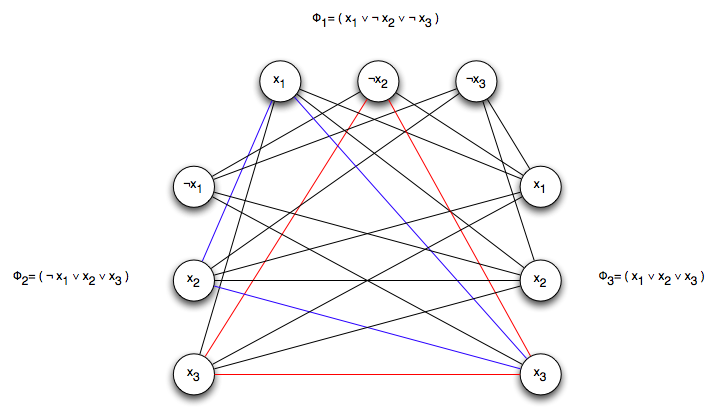
(1) $\Phi$ satisfiable $\Rightarrow G$ has $k$-clique. If $\Phi$ is satisfiable, then in the satisfying assignment, at least one literal in each clause is true. Each pair of those vertices must be connected, since we connect them all except complementary ones and ones within the same triple. Therefore $G$ contains a $k$-clique.
(2) $G$ has $k$-clique $\Rightarrow \Phi$ satisfiable. We can prove this by the contrapositive. If $\Phi$ is not satisfiable, then for any assignment there must be at least one clause not satisfied. This means that any selection of literals includes a complementary pair. These are not connected in $G$, so $G$ does not have a $k$-clique.
Alternatively, assume $G$ has a $k$-clique. It must include one vertex per clause/triple, and since no two can be complementary, we can set those literals true, creating a consistent truth assignment. Therefore, $\Phi$ is satisfiable.
What does this all mean?
Ok, so we’ve successfully performed a reduction. Since $\texttt{3SAT}$ is NP-complete and we have
we also know
so
That makes $\texttt{CLIQUE}$ also NP-complete!
Now recall our original chain:
And since $\texttt{3SAT} \equiv_p \texttt{CLIQUE}$,
Therefore, all of these problems are NP-complete!
This is how we’ve come up with so many NP-complete problems: we reduce from one known NP-complete problem to another. These chains form a web of reductions, like shown below.
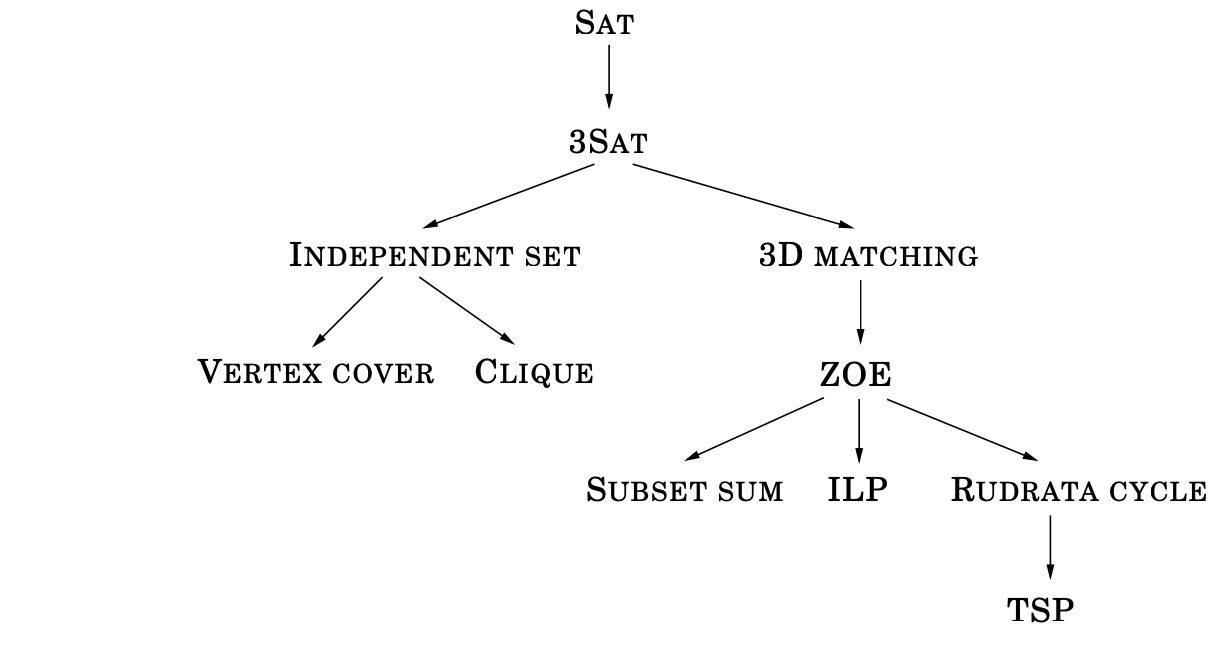
Why is this useful? Because NP-completeness gives us permission to give up! If you reduce your hard problem to a known NP-complete problem, you can (often justifiably) say no efficient algorithm likely exists—at least unless P = NP!