The Perles-Sauer-Shelah Lemma

and the VC Dimension

May 10, 2025

Introduction

The local animal hospital has a major problem. A misanthropic wizard has cast a spell on 8 dogs and 8 cats to turn them invisible, and now the shelter has to figure out which are which! With their knowledge of what ordinary dogs and cats are like, the veterinarians devise a scheme. They will measure each animal’s height and weight and plot it, and separate the data into two classes with a line.

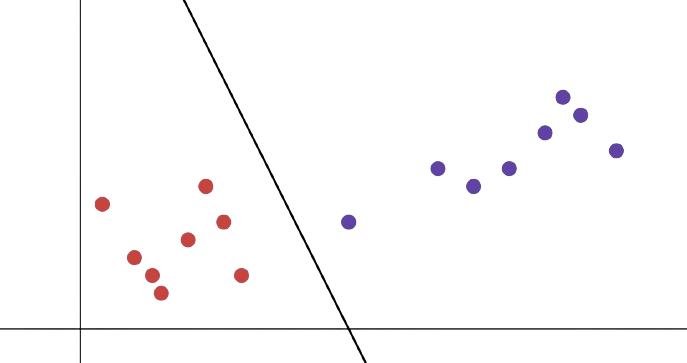
Cats vs Dogs plot — $x$ = weight, $y$ = height | red = cats, blue = dogs

Here, everything left of the line is a cat, and everything to the right is a dog. Setting the idiosyncrasies with their approach aside, the veterinarians have done what’s known as a very simple linear classification. A natural question is, how simple is this classification scheme? Clearly, we can separate out our cats and dogs, but what if the wizard had hexed some more unfortunate creatures, like frogs and lizards. How many creatures can we separate?

Binary Classification Models

A binary classification model is any function

\[f: \mathcal{X} \to \{0, 1\}\]

that gives a binary label to datapoints $\mathcal{X}$. Different models have different inherent complexities, and are capable of classifying different types of data. For example, a circular model, where any point within the circle is labeled red and any point outside the circle is labeled blue can be visualized as:

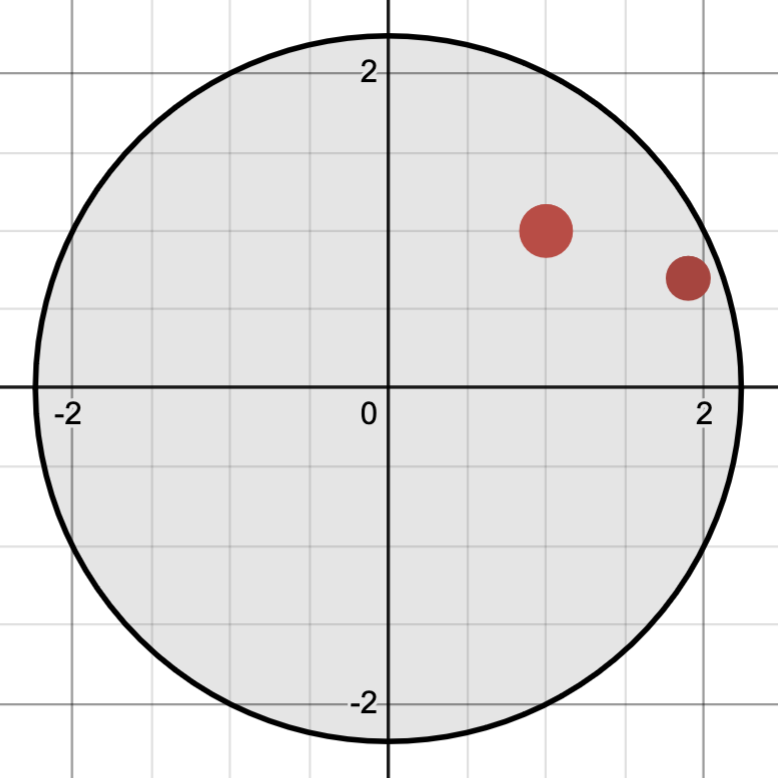
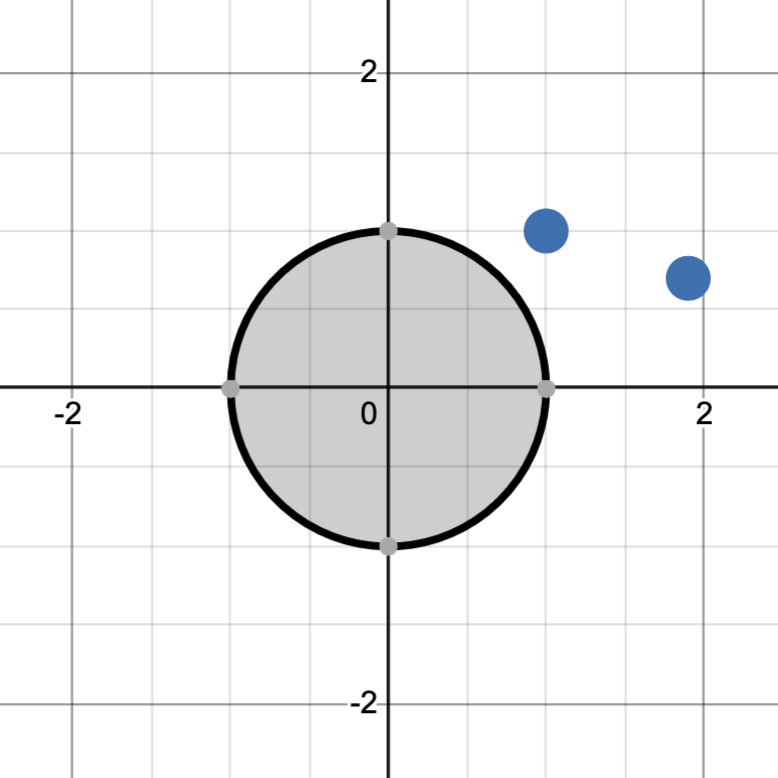
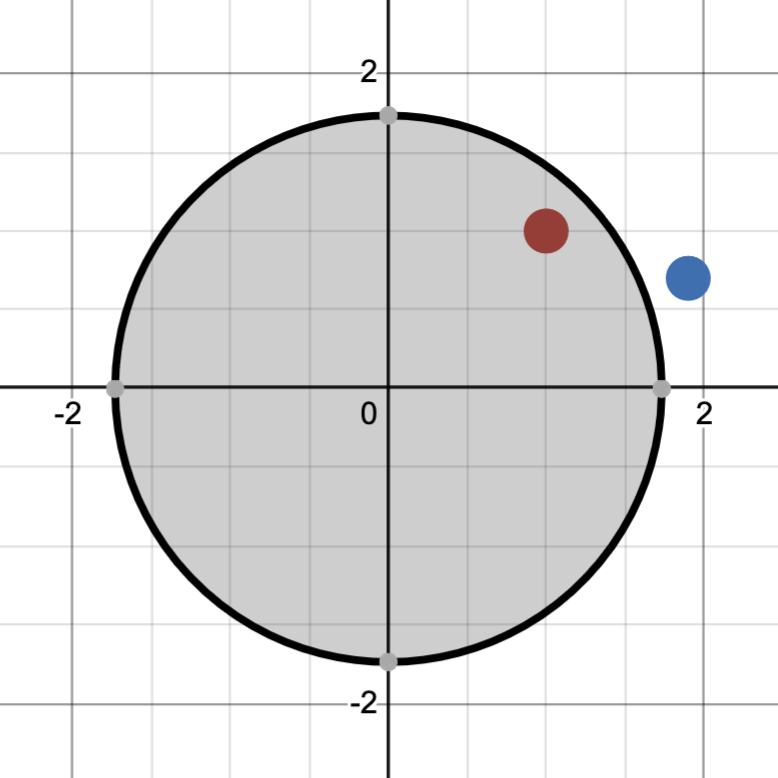
Notice however, that this model fails to classify a special case. If leftmost point is blue and the rightmost point is red, we have no way of classifying this by using different sized circles. A different model, a half-space of $\mathbb{R}^2$ that we label red if our point lies within it, has more classification power as we can generate all possible classifications.

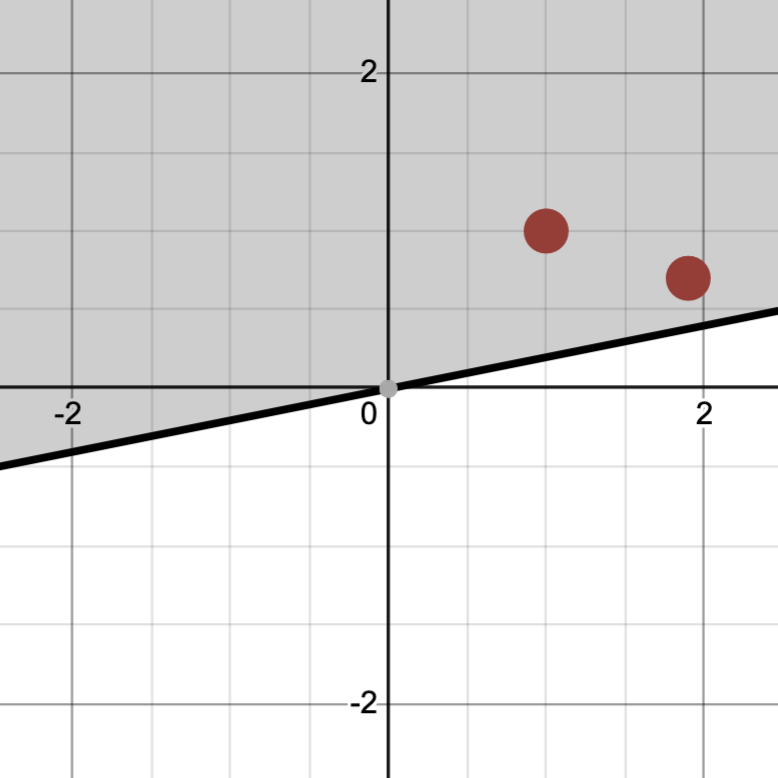
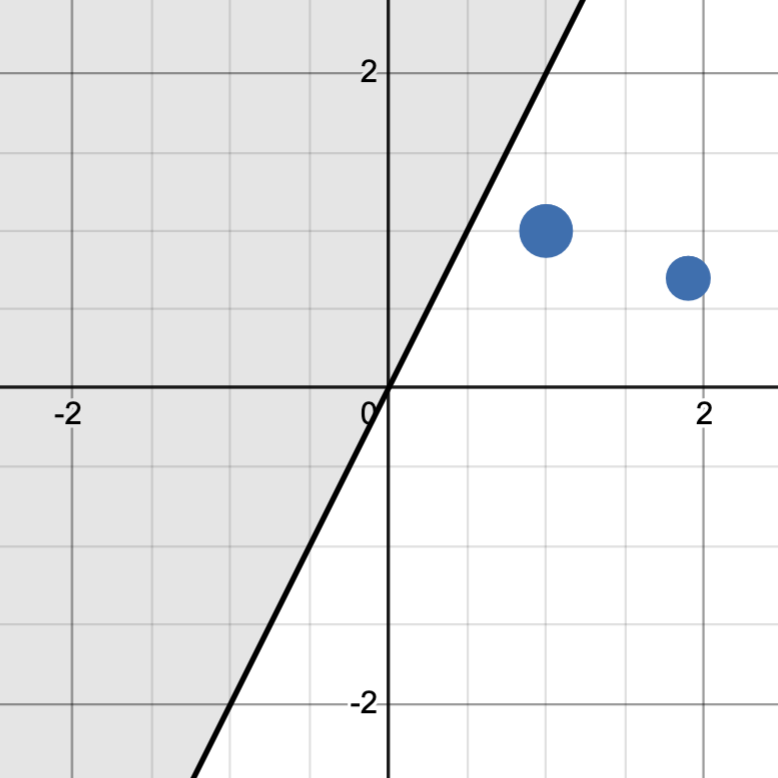
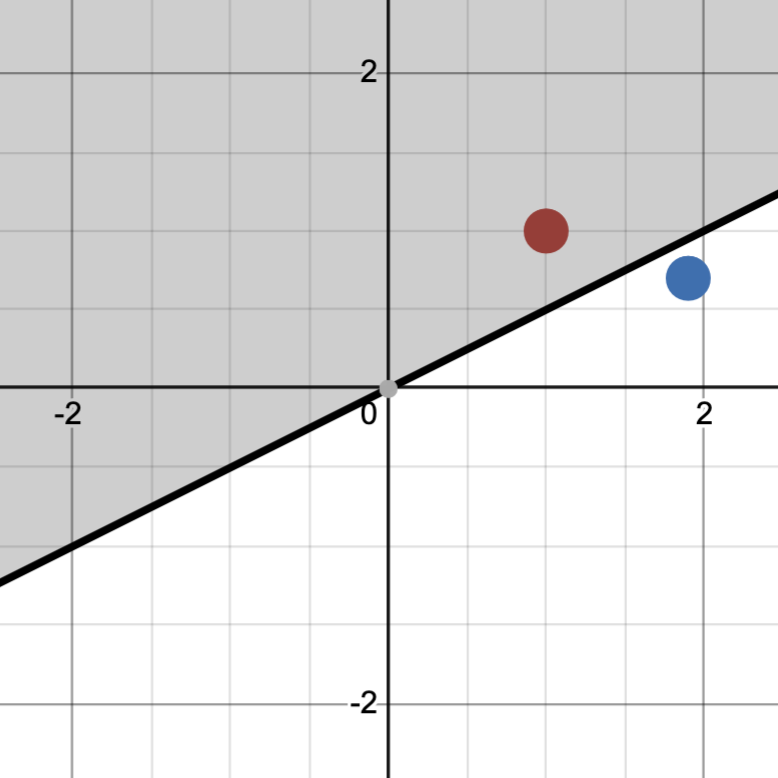
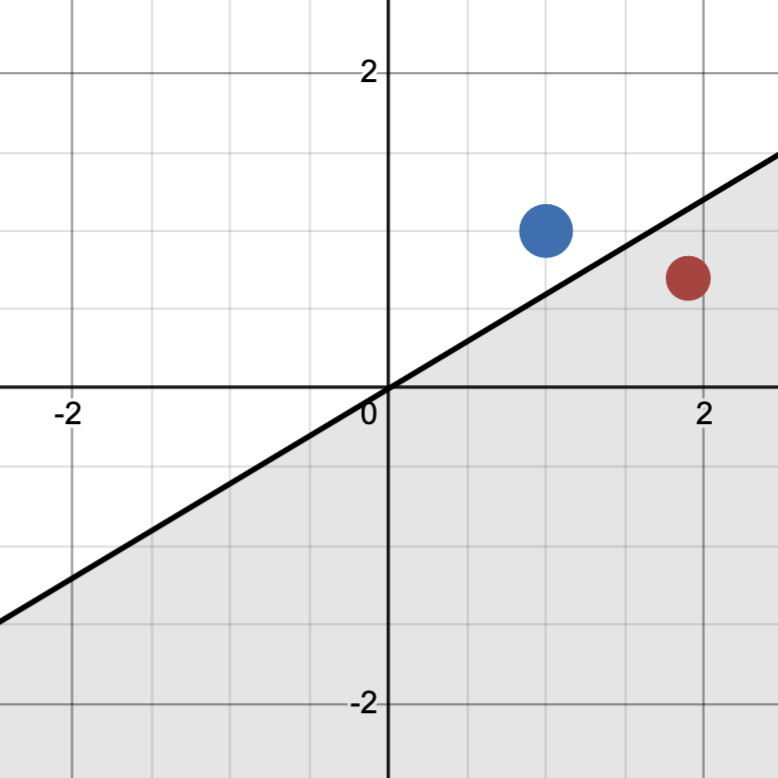
In this way, the second model is more expressive than the first. This motivates us to study the Vapnik-Chervonenkis dimension of a binary classification model (usually called the VC dimension), which is the way of measuring the expressivity of a binary classification model. We will now discuss a definition of VC dimension and an important lemma, and at the end we will connect this definition to the expressive power of a binary classification model.

VC-Dimension

We consider sets of binary vectors $A \subset \mathbb{Z}_2^n.$

Given an $n$-dimensional vector, we can create a set $S$ of coordinates of the vector. With this we define the projection $A\upharpoonright_S$ to be the vectors created by truncating each vector in $A$ to only include the coordinates of $S$. The example below shows a projection of a set $A$ onto the set

\[S = \{1, 3, 4, 5\}.\]

For example, if

\[A = \{[1,0,1,1,0,1], [0,0,0,1,0,1], [0,0,1,1,1,0], [1,1,1,1,1,0], [1,0,1,1,1,1]\}\]

Then projecting onto $S = {1,3,4,5}$ gives

\[A\upharpoonright_S = \{[1,1,1,0], [0,0,1,0], [0,1,1,1], [1,1,1,1]\}\]

In the example above, $A\upharpoonright_S$ is a small set. However if the projection $A\upharpoonright_S$ contains every possible vector in $\mathbb{Z}_2^k$, where $k = |S|,$ then we say that $A$ shatters $S$. The size of the largest set $S$ that $A$ shatters is the VC dimension of $A$.

How big can a set get before we shatter it? We can arbitrarily make a large set that isn’t possible to shatter by a set of size $k$ by taking every vector which has fewer than $k$ ones. Then, every projection will exclude the vector $(1, 1, 1, \dots, 1)$. Thus $A$ has size:

\[H(n, k) := \sum_{i=0}^{k-1}\binom{n}{i}\]

counted by summing over the number of vectors with $i$ ones, up to $k-1$. Though this does not shatter a set of size $k$, an important lemma states any bigger set will!

Perles-Sauer-Shelah Lemma

Statement: If $|A| > H(n, k),$ then $A$ shatters a set of size $k$

The proof is inductive on $n$ and $k$. For a base case we take a general $n$ and $k=1$. If $|A| > H(n, k) = \binom{n}{0} = 1,$ there are at least two different vectors in $A$ so there will be one coordinate that is different between them both. We use this to form the set $A\upharpoonright_S = \{[0], [1]\}.$ So regardless of $n$ we will always shatter a set of size $k=1.$ Now take any set with $|A| > H(n, k).$ We will project this onto the first $n-1$ coordinates $$ S = \{1, 2, \dots, n-1\} $$ to form the set $B = A\upharpoonright_S$ (we are effectively taking the vectors of $A$ and dropping the last coordinate). We will form a second set, $C$, which will be all the vectors in $A$ which are the same except have a different last coordinate. (For example if $(1, 0, 1, 1) \text{ and } (1, 0, 1, 0)$ are in $A$, then $(1, 0, 1)$ is in $C$). Notice that $$ |A| = |B| + |C|, $$ because $|B|$ will be nearly identical to $|A|$, except vectors with the same last coordinate in $A$ will merge to the same vector in $B$. Thus, we account for these via the vectors in $C$. Now if $$ |B| > H(n-1, k) $$ then $B$ shatters a set of size $k$, which means $A$ shatters a set of size $k$ (as we merely reintroduce an unused coordinate), which would finish the proof. So if $$ |B| \leq H(n-1, k), $$ using the identity $$ \binom{n}{i} - \binom{n-1}{i} = \binom{n-1}{i-1} $$ we have: $$ \begin{align*} |C| &= |A| - |B| \\ &> H(n, k) - H(n-1, k) \\ &= \sum_{i=0}^{k-1}\binom{n}{i} - \sum_{i=0}^{k-1}\binom{n-1}{i} \\ &= \sum_{i=0}^{k-2}\binom{n-1}{i} \\ &= H(n-1, k-1) \end{align*} $$ By induction, $C$ shatters a set of size $k-1$. However, $$ C \times \{0, 1\} \subset A, $$ so $A$ can shatter a set of size $k$ (notably, pick the shatter set of $C$ and include the last coordinate).

Conclusion

So now, given $n$ generally positioned points on the plane, every binary vector in $A$ represents the ways that we can possibly classify them. Perhaps this is determined by some function like a linear classifier, circular classifier, or something even more complicated.

If we can always find some subset (of size $k$) of these points such that we can classify these points in any way that we want, our classifier has shattered the points. In this way, the VC dimension loosely counts the expressivity of a model.

If we have a higher VC dimension, then we are able to classify a large subset of points in any way that we wish. If our model is based on some parameters, we are able to adjust them so as to get zero error depending on the true labels of the data points.

If we have a low VC dimension, then we are constrained with the shape of the model and cannot freely classify a large set of points in any way that we wish. The circle model above, for example, has a VC dimension of 1 because when we introduced two datapoints, we were not able to classify the blue-red case. The line, on the other hand, has a VC dimension of at least two because we could freely classify the two points.

Although it doesn’t seem to directly apply, taking the contrapositive of the Perles-Saur-Shelah lemma gives us a useful bound on the number of possible labelings of our set of points. If our VC dimension of our classifier is $k$ (i.e., $A$ does not shatter a set of size $k, k+1, \dots$) then $|A| \leq H(n, k),$ which has limiting behavior $\mathcal{O}(n^k)$. This bound is also tight, as we can create sets $|A| = H(n, k)$ by taking binary vectors with fewer than $k$ ones.

This helps give some more insight into how much VC dimension measures the expressivity of a model. A classifier on $n$ points with a VC dimension of $k$ can create up to $\sim n^k$ labelings. A classifier on the same points with a VC dimension of $k+1$ can create up to $\sim n^{k+1}$ labelings — an $n$-fold improvement!

In practice, however, increasing the VC dimension usually involves increasing the number of parameters of the model. The best models, therefore, are found by finding the greatest balance between complexity and expressivity.

References

Stasys Jukna. Extremal combinatorics: with applications in computer science, volume 571. Springer, 2011. Chapter 10
Wikipedia, Sauer–Shelah lemma, 2024 https://en.wikipedia.org/wiki/Sauer%E2%80%93Shelah_lemma
Wikipedia, Vapnik–Chervonenkis Dimension, 2024 https://en.wikipedia.org/wiki/Vapnik%E2%80%93Chervonenkis_dimension